Camera pixel size and photon collection

One of the trends that can be seen in microscopy in recent years has been the interest in imaging sensors with larger fields of view and smaller pixel sizes to maintain image detail when working at lower magnifications such as 20x. But are smaller pixels always better, or are there still conditions in which larger pixels are advantageous? In this article we consider pixel size and whether larger pixel sizes are still useful, and if so, where may this apply.

The Role of the Pixel

The role of a pixel in a sensor is to collect photons within a subunit of the imaging area and subsequently convert these to an electrical signal. By digitizing these signals, an image can be recreated from the values received at each pixel. The more efficient at gathering light and converting this light to an electrical signal, the more sensitive the detector can be. This has been a key driver of CCD and CMOS sensor technologies with processes such as back-illumination and use of microlens being examples of ways to boost the efficiency of these devices. The latest sensors available have quantum efficiencies reaching up to 95% i.e. 95% of incoming photons are converted into electrons in the photosensitive region of the silicon compared to devices a little over 10 years ago being limited to around 60% peak QE.

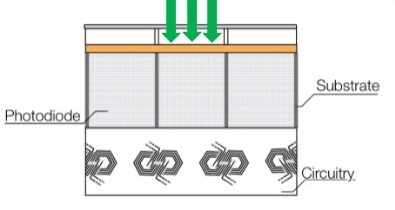
Figure 1: Modern sensor formats allow for high sensitivity by a combination of high photon collection efficiency and conversion and low noise electronics. This illustration shows a back-illuminated sensor in which the circuitry is beneath the photosensitive region and thus does not block light from reaching the region in which photons may be converted to electrons.

What effects does pixel size have on imaging?

Developments in sensor design and fabrication has enabled ever more smaller pixels to be packed into sensors. While more pixels can be better, there are trade-offs so the pixel size must be balanced to suit the needs of the application. There are three main aspects of how pixel size may impact imaging in addition to advances in other sensor technology enhancements such as back-illumination. These are summarized in table 1:

Table 1: Sensor parameters linked to pixel size and relationship to the image

Matching pixel sizes to microscope field of view and maintaining resolution is discussed more comprehensively in the article: Optimizing field of View and Resolution for Microscopy. In the following sections we will focus on pixel size and photon collection efficiency.

Pixel size and Photon Collection Efficiency

In table 2 we can see the pixel sizes of a range of current commercially available high performance imaging sensors that may be used for microscopy:

Table 2: The photon collection areas for each pixel for a range of different camera models

In general, CMOS sensors have smaller pixel sizes than EMCCD and CCD sensors. The CMOS sensor architecture also allows higher speeds and larger sensor sizes than CCD based designs. These qualities suit general fluorescence imaging applications allowing good image detail at common magnifications for cell biology studies and have made sCMOS the dominant detector technology for many microscopists.
Despite the rise of sCMOS detectors, EMCCD and CCD detectors have remained as the best option for some of the most challenging imaging applications and this looks set to continue for some time to come:
• EMCCD cameras use Electron Multiplication to effectively eliminate readout noise. This unique feature makes this sensor technology ideal for making precise quantitative measurements down to even a single photon such as single molecule imaging, but also for live-cell confocal imaging and super resolution systems.
• Deep cooled CCD cameras feature orders of magnitude less dark current than CMOS designs making them perfectly suited for long exposure luminescence experiments that are dark current limited and the slower readout of CCD is not a factor.

The large pixel sizes that these EMCCD and CCD cameras have also plays an important factor in why they remain suitable for these imaging scenarios. When photon collection is the priority, a larger pixel acts effectively as a larger catchment area for photons- feeding in more signal to the sensor. This is why the latest EMCCD sensor designs feature pixel sizes in the range of 13-16 µm which are natively suited to photon collection at high magnification e.g. 100x. Note that EMCCD cameras with smaller pixel sizes are available, but they have not gained any market traction as they do not provide application benefits over large pixel EMCCD, or to sCMOS camera options. In the following illustration, an iXon Ultra 888 EMCCD camera has a 4x higher native pixel area than a typical sCMOS camera and an 8x larger pixel area than the CMOS sensor.

Figure 2: Large pixel sizes are used in EMCCD and CCD cameras to gain advantage of the superior photon collection efficiency and improved probability of photon being detected. This example illustrates the relative sizes of 13 µm, 6.5 and 4.6 µm pixel.

What about the larger pixel sCMOS sensor formats?

There are some back-illuminated sCMOS cameras available with a pixel size of 11 µm pixel - which is a relatively large pixel when compared to typical CMOS cameras. These camera models, such as the Sona-11 sCMOS series, can take advantage of the light gathering power 3-fold higher than the 6.5 µm pixel size typically found in sCMOS cameras.

For some applications such as single molecule detection, and for high magnification, the larger pixel sCMOS cameras like the Sona-11 can offer some benefits:

• Higher sensitivity over the smaller pixel sCMOS cameras and field of view
• Higher speeds over a larger field of view, and increased image sampling compared to the EMCCD cameras.

However, for the more challenging single molecule experiments, the larger pixel size and high QE is not always enough. Electron multiplication process unique to EMCCD sensors boost the signal many fold prior to readout so the signal is far above the noise floor of the camera readout electronics and in practice proven to operate at photon levels below what is possible from any CMOS technology

Signal to Noise Comparisons

Here we compare 2 cameras with all factors the same (QE, read noise, dark current) other than their pixel size and compare the effect of pixel size on relative the signal to noise performance as light of a given illumination falls on each sensor.

Table 3: Simplified Signal to Noise comparison to illustrate the increase in the signal component provided by pixel size.

In the simplest comparison, camera 2 would look to provide a significantly higher signal to noise ratio since the signal component has increased for each pixel. To consider signal to noise for imaging cameras we need to use the following signal to noise equation to model the different signal and noise components involved:

Using this information we can plot the signal to noise against the number of photons, accounting for illumination intensity over the sensor by expressing photons on an area basis – in this example we will express per 13 µm² sensor area:

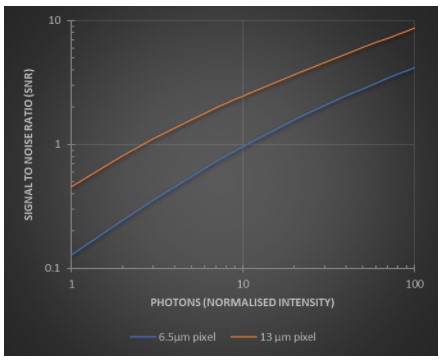Figure 2: A comparison the effect of pixel size on signal to noise performance of 2 sensors with all factors the same other than pixel size with incident light as photons normalised over per 13 µm.

From this we can see that the larger pixel does indeed allow for a higher signal to noise - some ~2.5x higher at 10 photons per 13µm². This will translate to the following benefits:

• Improved sensitivity – having a lower limit of detection
• Higher confidence in data at low signal levels
• Reduce exposures when light is more plentiful which is beneficial to many live cell studies.

We can then apply this to real-world camera examples:

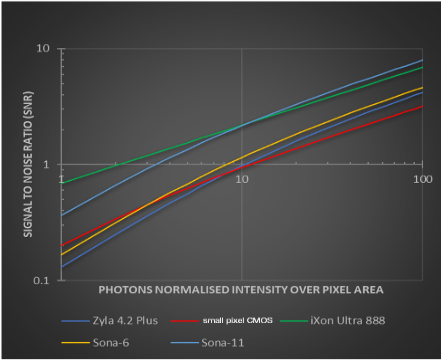Figure 3: Cameras developed for sensitivity and highest possible signal to noise feature large pixel sizes. Illumination corrected for pixel size by normalizing per 13 µm area.

In the comparison illustrated in figure 3 we can see that the cameras with larger pixels provide the better signal to noise figures such as the iXon Ultra 888 and Sona-11 models which aligns with their intended applications, that prioritize sensitivity and detection, over spatial resolution at low light levels. The other CMOS models with smaller pixels do not provide as high signal to noise ratios even though they have low noise levels. They will provide improved spatial resolution.

Can you use pixel binning to increase Signal to Noise Performance of small pixel CMOS sensors?

Smaller pixels can be binned – whereby the signal in a number of pixels may be pooled together to increase the overall signal level. A common example would be 2x2 binning which would group the signal for 4 pixels together as shown in figure 3. This works effectively for CCD in boosting speed and sensitivity as the serial nature of CCD allows each pixel value to be added before a read noise is added. Binning also works especially well outside of imaging for spectroscopy measurements as vertical binning may be applied without concern of losing resolution in the y axis.

Figure 4: 2x2 binning applied to sensor to boost photon collection across 4 pixels and the signal to noise ratio at the expense of spatial resolution.

The architecture of CMOS however is different. Each row has to be read out sequentially on a row-by-row basis before binning - meaning that for the CMOS sensors in use today binning will not deliver the benefits to signal to noise (and speed) that it does for CCD. Digital binning for sCMOS still combines he values for 4 pixels in the case of 2x2 binning, but the read noise also increases 2-fold since the 2 pixel rows are read out.

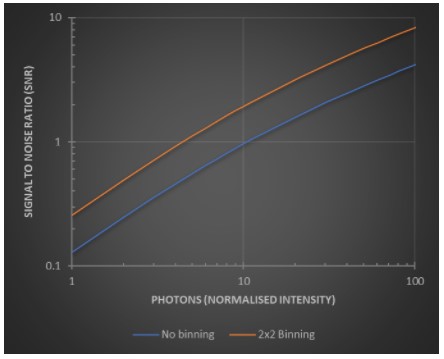Figure 5: While binning does not work as well for CMOS as CCD, it still allows a boost in signal to noise compared to without at the expense of spatial resolution.

For the smaller 4.6 µm pixels of the CMOS sensor 3x3 binning would be required to obtain the same photon collection area as a 13 µm pixel. 3x3 binning would thus increase read noise in this sensor type by a factor of 3.

What about optical matching?

Ideally the sensor size should fit within the uniform region available to the microscope and the pixel size would match the objective and magnification used for imaging. However, this is sometimes not the case for different combination of sensors, microscopes and application requirements. Additional post objective magnification may be used to avoid vignetting effects, or expand the field of view to cover that of a larger sensor area. The other application of additional magnification is to help meet optimal sampling of the image to meet or exceed Nyquist criteria e.g. adding a 2x lens with reduce the pixel size by x2 and help improve spatial resolution, but reduce the field of view. Thus, while useful, there are a number of considerations of using additional lenses in the optical system. This topic is discussed further in the article: Optimizing field of View and Resolution for Microscopy.

Largest Pixels mean Larger Well Depths for High Dynamic Range

The final aspect of imaging performance that is linked to pixel size that can be beneficial is the well depth of the sensor and how this can be used to allow for high dynamic ranges. When implemented correctly, larger pixels often allow larger signal handing capacities than is possible using smaller pixels.

Table 4: A comparison of the well depth of a selection of cameras. Note that maximum dynamic range may be restricted to certain modes available for each of the different camera models so is not presented here.

The impact in imaging terms will be that using small pixels may mean a low dynamic range that can result in oversaturation and lose of image information. Therefore, for applications in which a high dynamic range is important a well optimised sensor with larger pixel sizes may be more suitable than one with smaller pixels.

Imaging scenarios one may require high dynamic range include:

• Luminescence: experiments may involve very faint to high signal levels provide biologically relevant information on gene expression.
• Neurons – imaging neurons can sometimes pose a challenge as there can be a large intra-scene dynamic range due to strong signals in the central region of the neuron which distal regions exhibit low level fluorescence.
• Calcium Imaging – Given the vast number of functions of Calcium there are many different experiment conditions. For some of these, Calcium sparks and certain studies of cardiac and other cells they also require wide dynamic ranges.
• Large 3D volumes – when imaging large datasets, different regions of e.g. Zebrafish may have large differences in their signal level. This can make setting exposure and other image settings a matter of some trial and error to obtain a good image. A sensor with a wide dynamic range helps handle the dynamic nature of such datasets.

A further benefit of wide dynamic range is from a practical sense – a sensor with a wide dynamic range is more often in range and avoids saturation requiring less adjustment of settings such as exposure.

Conclusions

While there is interest in imaging cameras with small pixels to preserve image detail at low magnifications there is still very much the need for cameras with larger pixel sizes for low light applications.

• Cameras with small pixel sizes suit low magnification studies. Many models available that work under these higher light regimes.
• The 6.5 µm pixel size that is common to many scientific grade microscopy cameras provides a good balance between photon collection and resolution for typical fluorescence based applications.
• When looking to get the best possible sensitivity from a detector, cameras with large pixel sizes are the most applicable e.g. for single molecule imaging and luminescence
• Binning can be used to increase signal to noise in both CCD and CMOS sensors, however for CMOS sensors there is less benefit from binning as there is for CCD.

There is no one camera that does all imaging scenarios better than every other camera. Thankfully there are now a range of cameras that can be selected to suit different applications that need for example the highest spatial or temporal resolution, or the best possible sensitivity. This means that it is important to consider the application needs first and foremost and not assume that the latest camera model with the largest sensor and most megapixels will be the best option.