Étendue and You: Maximising Efficiency in Astronomical Wide Field Imaging

Étendue is a property of observatories that must be considered when optimising for wide field imaging surveys and other data-intensive modes of observing. In this article we’ll look at étendue, what it represents in astronomy, how it can be maximised, and how an astronomer’s choice of camera will affect this important property of their overall system. Sometimes étendue is also known as etendue or grasp.

For any system of optics that can receive light from an external source, étendue is a conserved quantity describing how much energy the optical system can accept [e.g. 1,2]. Mathematically, étendue is the product of the source’s emitting area, A, and the solid angle contained within the optical system’s useful field of view, Ω. Equivalently, ε=AΩ in units of m2deg2. For a telescope it helps to follow Huygen’s principle for light waves and think of the light source as the combined wavefront of all astronomical sources in the field of view at the entrance to the telescope aperture. Wavefronts not entering the telescope are not collected and do not matter. The source’s emitting area, A, then simply becomes the area of the telescope aperture. As a function of the telescope’s field of view (FoV), Ω depends mostly on the telescope’s focal length and the size of its sensor or field stop (Fig. 1).

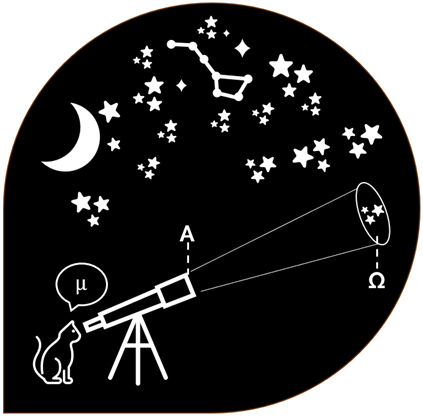
Figure 1 - The étendue of this feline astronomer's telescope is the product of its primary aperture and the solid angle of the sky contained within its field of view.

The definition of étendue can be made more specific for astronomical telescopes, however, as light is merely the carrier of the information that astronomers are interested in recording and analysing. Étendue may therefore be reframed in astronomy as the data flow through an optical system [e.g. 1,2]. In other words, étendue can be considered a measure of the information gathered per second by an astronomical observatory with a given sensitivity, FoV, and angular resolution. It’s important to highlight the time component in this definition, because the rate of information collection by an astronomical observatory is often proportional to its étendue. As a result, the efficiencies of information intensive observing methods like wide field imaging surveys, time domain monitoring campaigns, and searches for astronomical transients rise and fall with étendue as well.

In this context, considering both A and Ω in more detail can help us identify ways to optimise an observatory and its instruments for étendue and efficient astrographic observations.

Sensitivity

Rather than simply the collecting area of the telescope, A is an effective wavelength-dependent collecting area that represents the data collection rate of an observatory given the size of its aperture, the transmission efficiency of its optics, and both the sensitivity and efficiency of its imaging camera. Mathematically, we might state this as:

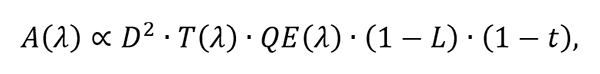
where λ is the observed wavelength, D is the diameter of the telescope’s primary aperture, T(λ) is the transmission efficiency of the telescope’s optical train, QE(λ) is the quantum efficiency of the camera’s sensor, L is the proportion of signal lost to various noise sources in the camera, and t is the proportion of up-time for the camera that is lost to operational overheads such as sensor readout. From this formula we can see that there are more ways to increase A than simply enlarging the telescope primary aperture. Using a camera with a higher QE, lower noise, and a higher integration duty cycle (i.e. lower overheads) can increase the rate of survey data acquisition. On this last point, astronomers may consider using a camera with an sCMOS or frame transfer CCD sensor over one with a traditional CCD sensor as the first two of these options offer much faster image readout. Increasing T(λ), the transmission of the telescope, is one way to increase A that should be considered carefully, as in some cases extra corrective optics are needed to ensure high quality off-axis imaging capability and provision of a large useful FoV. In this case, an increase in A may result in a reduction of Ω. Operationally, an increase to A should reduce the quantity and/or length of exposures needed to complete an imaging sequence for a particular tract of sky. By extension, less time spent observing each pointing in a survey means more sky can be covered more rapidly.

Field of View

As mentioned previously, Ω is directly related to an observatory’s useful FoV and can be boosted by reducing the telescope’s effective focal length and/or enlarging the camera’s sensor. Again, increasing an observatory’s useful FoV may require the introduction of additional optical components to reduce off-axis aberrations. Additional components will increase transmission losses along the optical train and may reduce A. As a result, the optical design of a wide field astrographic telescope must be considered carefully to simultaneously maximise both A and Ω. If a telescope’s camera sensor is smaller than the useful FoV of the telescope it’s mounted to, replacing the camera with another that has a larger sensor is a simple way to access a wider FoV. Operationally speaking, increasing Ω allows bigger tracts of sky to be observed at each telescope pointing, reducing the number of pointings required to cover a given survey area.

Resolution

Returning to our consideration of étendue as a measure of the information flow through an observatory, it is critical to recognise how the resolution of a telescope and its camera also play their part. If we consider an absurd extreme, what good is there in having a very wide FoV and large Ω if it’s only sampled by a single very large camera pixel. In this case, photon collection is very efficient but all information about the spatial distribution of light sources in the field is lost. Rather than simply Ω, then, étendue is proportional to Ω/dΩ where dΩ is the smallest subunit of Ω that can be resolved. In isolation it looks like minimising dΩ (i.e. maximising resolution) by minimising the camera’s pixel size is a good way to maximise the amount of information acquired in each image, but of course there are practical limits to how small dΩ can get before we start to run into problems.

Choose Small Pixels, but Not Too Small

The limiting angular resolution of a wide field survey telescope is determined by either the Full Width at Half Maximum (FWHM) of its seeing-limited point-spread function (PSF), θ, or the plate scale of its camera, p, whichever is larger. Mathematically speaking, dΩ∝〖max(θ,p)〗^2. Here, the camera’s plate scale is the projected angular size of a pixel on-sky, usually given in arcseconds per pixel. As very wide field adaptive optics correction (currently) has limited efficacy, most survey observatories operate in the seeing-limited regime.

To estimate the ideal pixel size needed for the camera on an astrographic telescope, we need to determine the physical size of the seeing-limited PSF on the sensor. Under diffraction-limited conditions the size of a telescope’s diffraction-limited PSF is given by Θ=1.22∙f#∙λ [3], where f# is the telescope’s focal ratio and λ is the observed wavelength. A diffraction-limited point source observed at 550 nm and focused by an optically fast f#=2 astrographic telescope will produce a point spread function with a FWHM of 1.342 µm, which is about 10 times smaller than the typical pixel of a CCD sensor. Under seeing-limited conditions, the PSF will be broader, but for any telescope with an aperture <1 m in size observing in typical good seeing conditions (<2 arcseconds) the seeing-limited FWHM will never be more than ~15x larger than the diffraction-limited FWHM. This means that under good natural observing conditions the PSF of such an astrographic telescope is likely be somewhat undersampled by a sensor with pixels of size typical for a CCD (i.e. ~10-15 µm).

For sufficiently bright targets, mild undersampling concentrates their light into fewer pixels and boosts the delivered signal-to-noise ratio (SNR) of the data. This is the only real benefit to undersampling the PSF, however, and doing so may bring multiple drawbacks:

1. Undersampling of the focal plane by the sensor’s pixels results in loss of spatial information and a decrease in Ω/dΩ that may negate any boost in SNR and reduce étendue.

2. If undersampling is severe, prior knowledge of the observed field and extra data reduction steps may be required to deblend the signal detected from multiple sources in a single pixel. Accurately achieving this is not trivial.

3. By their nature, ground-based observations also detect photons scattered or emitted by the background sky. The shot noise of these photons adds in quadrature to the noise from other sources that affect the detection of photons from objects within the imaged field. Because larger pixels detect more background photons per pixel, the shot noise of the background is also increased. Greater per-pixel background shot noise for larger pixels reduces their sensitivity to the faintest targets relative to that of smaller pixels with otherwise equivalent performance. Additional noise in the case of large pixels will reduce both A and étendue as more and/or longer integrations are needed to image fainter targets.

For the reasons stated above, some may consider using a camera with an sCMOS sensor over that with a CCD sensor when aiming to maximise étendue, as the pixels in sCMOS sensors are typically smaller. As a result, they are better suited to optimally sampling the smaller focal spots of optically fast astrographic telescopes. Mild undersampling of the focal plane is not a death sentence for an astrographic telescope, however. In fact, many successful surveys have been conducted this way [e.g. 4,5]. When designing or upgrading such facilities, however, opting for a sensor with smaller pixels may be worth considering.

Of course, having pixels that are too small may also reduce étendue. Small pixels hold less charge than large ones, which may limit the dynamic range of each exposure and necessitate observation and stacking of more images to reach a survey’s target depth. Each acquisition will come with some overhead, and even small increases in the number of exposures needed per tract of sky may add up to a lot of extra time needed to complete a large wide field survey. If p≪θ, the camera’s pixels will oversample the telescope’s PSF, which under seeing-limited conditions has angular resolution limited to θ. In this case the collected light is spread thinly over a greater number of camera pixels, reducing delivered SNR in each image (A) without providing any boost to spatial resolution (Ω/dΩ). Ideally, an observatory should be designed such that the pixels of its camera sensor are sampling the telescope’s focal plane according to Nyquist-Shannon sampling theory, where 2 to 3 pixels sample θ [e.g. 6]. When the camera’s pixels are optimally sampling the telescope’s focal plane, observations achieve their peak resolution without needlessly sacrificing the SNR of the data. In other words, an optimal balance is struck between A and Ω/dΩ to maximise étendue.

References

1. Ofek & Ben-Ami 2020, Publications of the Astronomical Society of the Pacific, 132, 125004

2. Berry et al. 2016, “Big! Fast! Wide! Sharp!: The Story of the Rowe-Ackermann Schmidt Astrograph”, Version 1, (Torrance, CA: Celestron), https://s3.amazonaws.com/celestron-site-support-files/support_files/rasa_white_paper_web.pdf

3. Texereau, J. 1984, “How to Make a Telescope”, (2nd English Edition; Richmond, VA: Willman-Bell)

4. Ratzloff et al. 2019, Publications of the Astronomical Society of the Pacific, 131, 075001

5. Tonry et al. 2018, Publications of the Astronomical Society of the Pacific, 130, 064505

6. Shannon 1949, Proc. of the IRE, 37, 10