Quantum Simulation Breakthrough: Ytterbium Atoms in Optical Lattices

Researchers from Kyoto University led by Prof. Yoshiro Takahashi and co-workers developed a new approach to measure spin correlations between nearest neighbor of ultracold fermionic ytterbium atoms with six spin components in an optical lattice [1].

Hubbard model and phenomena which appeared at low temperatures: Mott states, spin correlated states

The Hubbard model is widely known as a lattice model that can well describe electrons in solids. At low temperatures, a Mott state appears, in which atoms are isolated inside lattice. Furthermore, at low temperatures, spin correlations between neighboring atoms arise due to virtual hopping, which is the origin of antiferromagnetic phases and superconductivity. Although the Hubbard model is appropriate to describe such transition, it is difficult to solve numerically, especially for large dimension and spin components, because realistic systems are too large to be solved with available computational resource [2].

Measurement of spin correlation between neighbor sites

In systems with multiple degrees of freedom, the ground state is not known even theoretically at absolute zero. Kyoto University group used Fermi isotopes of ytterbium atoms with six spin degrees of freedom and detected spin correlations between neighboring sites in an optical lattice (Fig.1) [1]. They measured the difference in the number of atoms between spin-singlet and spin-triplet by removing the spin-singlet atom pairs by resonant light and observing the number of remaining atoms. Furthermore, they compared the experimental data to the numerical calculation by theoretical collaborators, the temperature realized in the 1D system is about 1/10 of the tunneling amplitude.

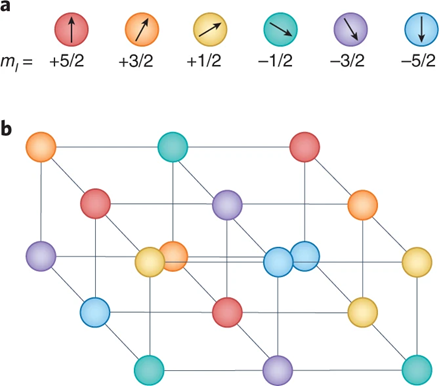
Fig. 1. SU(6) fermionic Hubbard model. Taken from Nature Physics volume 18, pages 1276–1277 (2022).

Observation of ultracold atoms using an Andor EMCCD camera

All laser cooling experiments are performed in a vacuum chamber. Therefore, the only way to manipulate the samples are magnetic fields and light. The measurement of the number of atoms is done by measuring the absorption of resonance light. To do this, it is necessary to observe the ratio among two light beams, one with atoms and the other without atoms (Fig. 2) [3].

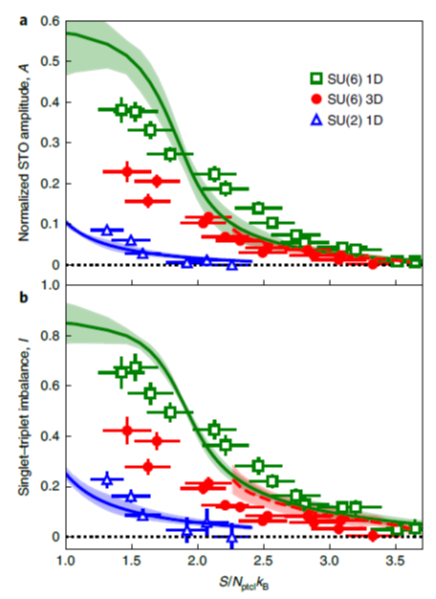
Fig. 2. Entropy dependence of the nearest-neighbour correlations. Green squares (SU(6) 1D), red dots (SU(6) 3D), and blue triangular (SU(2) 1D) are shown. Solid lines show numerical calculations without fitting parameters. Taken from Nature Physics volume 18, pages 1356–1361 (2022)

However, interference fringes originating from slight vibrations of the experimental setup disturb this measurement. To obtain a high-quality image, the two images should be acquired at a high speed of less than 0.1 ms, which is largely a function of the quality of the electrical implementation, such as the AD converter, rather than the performance of the CCD chip. In this study, this difficulty was overcome by using the Andor DU-897.

Quantum simulator of many-body systems

Quantum many-body systems are simple models, but at large scales, they cannot be practically solved on classical computers due to problems of computational resources and time. This was pointed out by Feynman, who at the same time proposed to "simulate" the system in a system that follows quantum mechanics to solve it efficiently [4]. The agreement between experiment and theory in this study indicates that cooled atoms in optical lattices can serve as good quantum simulators.

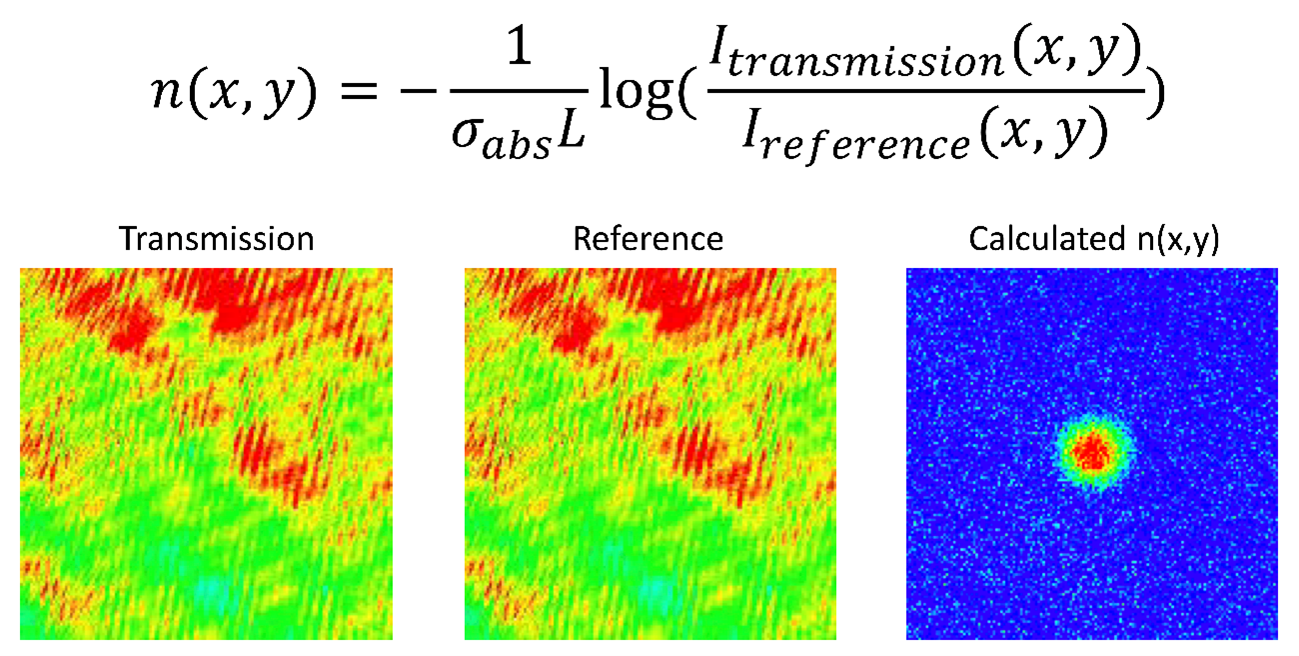
Fig. 3. Typical images of transmitted and reference lights.

References and Further Reading

[1] Taie, S. et al. Observation of antiferromagnetic correlations in an ultracold SU(N) Hubbard model. Nat. Phys. 18, 1356–1361 (2022).

[2] Altman, E. et al. Quantum Simulators: Architectures and Opportunities. PRX Quantum 2, 017003 (2021).

[3] Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).

[4] Feynman, R. P. Simulating physics with computers. Int J Theor Phys 21, 467–488 (1982).