What is spatial resolution and pixel size in CCD cameras?

The resolution of a CCD is a function of the number of pixels and their size relative to the projected image. CCD arrays of over 1,000 x 1,000 sensors (1 Mega-pixel) are now commonplace in scientific cameras. The trend in cameras is for the sensor size to decrease, and cameras with pixels as small as 4 x 4 microns are currently available in the consumer market. Before we consider the most appropriate pixel size of a particular application, it is important to consider the relative size of projected image to the pixel size to obtain a satisfactory reproduction of the image.

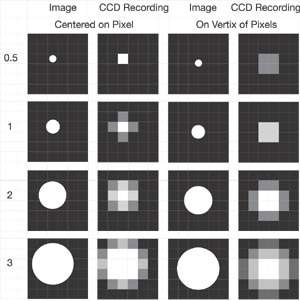
Consider a projected image of a circular object that has a diameter smaller than a pixel. If the image falls directly in the centre of a pixel then the camera will reproduce the object as a square of 1 pixel. Even if the object is imaged onto the vertices of 4 pixels the object will still be reproduced as a square only dimmer - not a faithful reproduction. If the diameter of the projected image is equivalent to one or even two pixel diagonals the image reproduction is still not a faithful reproduction of the object and critically varies on whether the centre of the image projection falls on either the centre of a pixel or at the vertex of pixels.

It is only when the object image covers three pixels do we start to obtain an image that is more faithfully reproduced, and clearly represents a circular object. The quality of the image is also now independent of where the object image is centred, at a pixel centre or at the vertex of pixels. Nyquist's theorem, which states that the frequency of the digital sample should be twice that of the analog frequency, is typically cited to recommend a "sampling rate" of 2 pixels relative to the object image size. The Nyquist theorem deals with 2-dimensional signals such as audio and electrical signals and it is unsuitable for an image, which has three dimensions of intensity versus x and y spatial dimensions.

Modulation Transfer Function

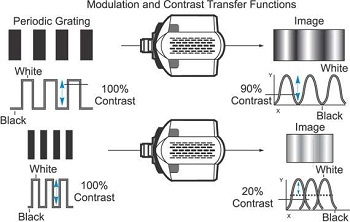
In addition to the discrete pixels, other factors such as the quality of the imaging system and camera noise all limit the accurate reproduction of an object. The resolution and performance of a camera within an optical system can be characterized by a quantity known as the modulation transfer function (MTF), which is a measurement of the camera and optical system’s ability to transfer contrast from the specimen to the intermediate image plane at a specific resolution. Computation of the modulation transfer function is a mechanism that is often utilized by optical manufacturers to incorporate resolution and contrast data into a single specification. This concept is derived from standard conventions utilized in electrical engineering that relate the degree of modulation of an output signal to a function of the signal frequency.

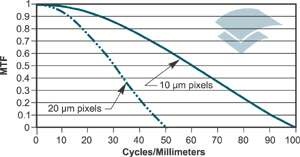
A typical MTF curve for a CCD camera with a 10x10 and 20x20 micron pixels is shown below right. The spatial frequency of sine waves projected onto the sensor surface is plotted on the abscissa and the resultant modulation percentage on the ordinate. The limiting resolution is normally defined as the 3 percent modulation level.

Adequate resolution of an object can only be achieved if at least two samples are made for each resolvable unit (many investigators prefer three samples per resolvable unit to ensure sufficient sampling). In the case of the epi-fluorescence microscope, the resolvable unit from the Abbe diffraction limit at a wavelength of 550 nanometers using a 1.25 numerical aperture lens is 0.27 microns. If a 100x objective is employed, the projected size of a diffraction-limited spot on the face of the CCD would be 27 microns. A sensor size of 13 x 13 micron pixels would just allow the optical and electronic resolution to be matched, with a 9 x 9 micron pixel preferred. Although small sensors in a CCD improve spatial resolution, they also limit the dynamic range of the device.